Multiplicación de funciones
Sean f y g dos funciones reales de variable real, y definidas en un mismo intervalo. Se llama función producto de f y g a la función definida por:

En primer lugar, debemos estar seguro que existe una intersección de los dominios de las funciones a ser multiplicadas.
Recuperado de: https//www.slideshare.net/ABELEO/intervalos-1571515
En segundo lugar, se debe multiplicar las respectivas reglas de correspondencia
Ejemplos
1) Sean las funciones:
Hallar (f*g)(x)
2)
Dadas f, left parenthesis, x, right parenthesis, equals, 2, x, minus, 3 y g, left parenthesis, x, right parenthesis, equals, x, plus, 1, encuentra left parenthesis, f, dot, g, right parenthesis, left parenthesis, x, right parenthesis.
(f⋅g)(x)=f(x)⋅g(x)=(2x−3)⋅(x+1)=2x2+2x−3x−3=2x2−x−3
Autor: Creación propia
3)
e
765474y
left parenthesis, c, dot, d, right parenthesis, left parenthesis, y, right paren
left parenthesis, c, dot, d, right parenthesis, left parenthesis, y, right paren





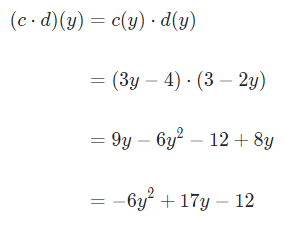
Comentarios
Publicar un comentario